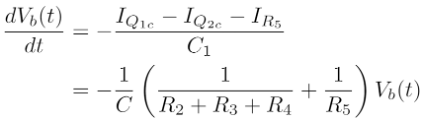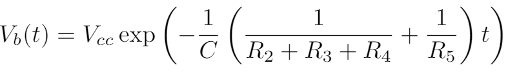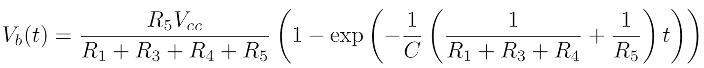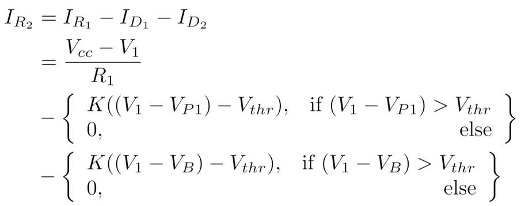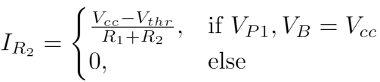DHQ: Digital Humanities Quarterly
Editorial
Playing in the Gap:
Analog Programming and the First Video Game Console
Zachary Horton, University of Pittsburgh
Levi Burner, University of Maryland
Introduction
In this essay we explore the relationship between code and the physical world by examining
a media artifact that, we contend, challenges some common assumptions about this relationship.
We wish, in particular, to challenge the preconceived notion of a strong dichotomy
between code and external world: that code is the result of an encoding, a translating
of some aspect of the physical world into a discrete symbolic system that, when executed
on computational hardware, follows its own rules. Code is commonly, if implicitly,
represented as an interiority intimately intertwined with, but ontologically and pragmatically
delineated from the exterior, analog environment. In this model, computational hardware
bridges the gap between these two worlds — between, that is, the symbolic representation
and what it accomplishes, the digital and the analog. In what follows we interrogate
this formulation, as well as the attendant assumption that code must always be digital,
by examining a unique and culturally significant example of a video game: Volleyball,
coded for the first home video game console, the Magnavox Odyssey. The Odyssey was
developed from 1966 to 1969 by Ralph Baer and a small engineering team at Sanders
Associates and released by Magnavox in 1972. Unlike nearly every other video game
console released since, the Odyssey lacked a microprocessor: its internal signals
were continuously variable voltages, not quantized bits. While this categorizes it
as an analog device, in what follows we argue that its analog architecture does not
preclude it from possessing digital logic, nor from being programmable. Situating
the Odyssey within the historically significant, but academically under-examined tradition
of analog computing, our purpose is threefold: First, we wish to draw attention in
critical code studies to the tradition of analog computing, offering an examination
of many parallels between digital and analog programming. Second, we explore the
unique affordances [1]of the Odyssey as a programmable platform that integrates logic and material structures
in a unique and historically important way. Finally, we argue throughout for an expanded
concept of code and coding that challenges the centrality of the digital and more
expansively engages the roles of users and physical environments as components of
coded systems.
The Odyssey came bundled with twelve games and many insertable game cards, television
overlays, decks of cards, game boards, and other “playing aids” that supplemented
the on-screen graphics, and which are necessary to fully constitute the games. Shortly
after launch, a collection of six additional games was released to the public through
Magnavox retailers as an add-on purchase for Odyssey owners. Volleyball, the specific
program we analyze here (Figure 1), was one of those six add-on games.[2] It was commercially released in its own product box packaged with a game card (#7),
an instruction sheet, and an overlay in two sizes (for 19” and 26” televisions).
Like almost all other Odyssey games, Volleyball requires the players to place a thin
plastic overlay over [3]their television screen to provide additional (static) graphics for the on-screen
environment and to produce various optical effects such as altering the color of the
television’s graphics, hiding them with opaque layers, or brightening them with clear
sections. Volleyball’s overlay is relatively simple, composed of a single color background,
serve locations, net location, and images of volleyball players in action (Figure
1). Judged by number of components, this was the sparest game in the pack. We’ve
chosen to analyze this particular game not because it was especially popular or influential,
but because it is representative of analog programming at the time, makes use of many
of the Odyssey’s capabilities, and possesses a number of unique features that we consider
particularly illuminating of both the differences and intertwining between analog
and digital systems[4]. In particular, Volleyball is a useful object with which to explore the gap between
the simulation produced by coded games and the actual milieus and processes to which
they refer.
Figure 1: Volleyball being played, with overlay in place. Photograph by Zachary Horton.
In order to explore the relations between code and world, staged by Volleyball and
the Odyssey, we will consider and demonstrate several symbolic schemas for representing
the game’s code, each illuminating a different “level” of operation, scale, and abstraction.
First, we examine the Odyssey’s hardware, in which much of its digital logic and analog
computation is encoded as a series of circuits and flows. Second, we consider Volleyball’s
code as a series of mathematical functions that link hardware to symbolic operations.
Third, we demonstrate the logic flow layer of the program using analog computation
notation (“program blocks”) and compare this to coding in today’s digital programming
languages. Finally, we consider elements of the game’s algorithm that are addressed
directly to players and require various real-world bodies, objects, and interfaces
to fully run the program’s main loop. Along the way we examine the affordances of
each symbolic system and ontological layer for revealing meaning in the code, as well
as the limitations of each.
We hope that this discussion will also serve as a primer on the nearly forgotten media
ecology of analog computation and programming. We argue that Volleyball “plays in
the gap” between simulation and reality, digital and analog, code and world, and thereby
provides us with an exciting object with which to think through not only the historical
birth of home video games (as precursor to home computing), but also the material
affordances and transitive capacities of all code, analog or digital. This examination
of an Odyssey game will lead us to a characterization of its programming as assemblage-making[5]—a kind of code that runs on different levels simultaneously, accepts feedback from
their unique properties, and composes new channels for communication between levels.
We hope that this vision of code as material, multiscalar, and porous[6], what we call multi-level coding, will inspire programmers to explore similar modalities
in the future.
Level 1: Hardware
Hardware, or an active substrate capable of running code, must be able to receive
signals, transform them in accordance with their content, and usually produce some
sort of output, either digital (such as a string of serial data) or analog (such as
light emitted from a screen or sound emitted from a speaker). Media theorist Friedrich
Kittler, in his notorious essay, “There is No Software,” notes that “all code operations,
despite such metaphoric faculties as call or return, come down to absolutely local
string manipulations, that is, I am afraid, to signifiers of voltage differences”
(Kittler 1997, 150). In Kittler’s formulation, code functions culturally to conceal
its own signification, to “obscure hardware with software,” a kind of conjuring trick
pulled off through the stacking of many “interfaces between formal and everyday languages.”
(Kittler 1997, 150). If code’s actual signifieds are physical state changes, software
misdirects its human users to invest meaning elsewhere, in an abstract, symbolic space.
This seems to disturb Kittler because code pretends to a universality (a Turing machine)
that subsumes and transcends the physical world when in fact it engages only a small
portion of it: that which is programmable using discretized hardware configurations.
Kittler goes on to argue that nonprogrammable systems (continuous or analog structures
such as “waves,” “wars,” and “beings”) are not only more characteristic of “the world,”
but also far more dynamic in connectivity and growth. Code, he implies, is inadequate
to represent or capture such processes because it is functionally limited by the discrete
hardware to which it reduces, and “only computations done on nonprogrammable machines
could keep up with (the continuous systems of the world).” Kittler’s argument is
more nuanced (and perhaps beguiling) than is usually acknowledged, or indeed that
his essay’s polemic title would suggest. While there are a number of ways to answer
(or dismiss) his claims, we would like to explore them in a novel way by examining
code that performs its computations on precisely the sort of “nonprogrammable machine”
that Kittler seems to rule out: the Magnavox Odyssey, a platform whose physical substrate
is fundamentally continuous, or analog, rather than discrete, or digital.
The Odyssey is not constructed out of silicon chips that quantize voltages in on-off
gates at discrete times. Rather, it consists of an electrically conductive set of
nested circuits that elicit continuous and discontinuous waves and modulate these
signals at every moment, thus retaining their continuous (analog) nature. Nonetheless,
it processes sets of instructions that deftly weave digital logic with continuous
processes by converting between the two internally, and providing output signals that
retain both characters. A fully digital computer can, through numerical integration,
analog-to-digital converters, and digital-to-analog converters, approximate behavior
of analog systems; yet as Kittler and audiophiles who shun digital formats for vinyl
have long argued, approximation is not ontology, and what is at stake is being, or
presence, itself.
The Odyssey is, at its hardware level, an analog device, and yet it is programmable.
As such, it is a member of a class of devices once significantly more common than
digital computers, yet contemporaneous with them: the electronic analog computer.
The general neglect of analog computers, by both popular culture and scholars, is
perhaps at least partially attributable to a “progress narrative” constructed by the
nascent digital computer industry in the 1950s for marketing purposes, which was enthusiastically
taken up by the popular press of the time. This discourse suggested, contrary to
professional discourse, that digital computers were superior successors to analog
computers rather than contemporaneous machines suited to different sorts of tasks
(Kline 2019). Part of the allure of the digital machines was that they seemed analogous
to brains and were in fact usually called “electronic brains.” The analog computer,
as we will see, functions by programming dynamic systems that were analogous to those
about which they computed. Ironically, then, their greater analogic flexibility rendered
them narratively less sensational than digital computers, with their single striking
analogy. This asymmetric popular coverage has been inherited by scholars today.
Another discursive trend has also served to diminish the historical visibility of
analog computing, and that is our contemporary popular characterization of code.
Code captures the imagination because it is expressed in linguistic terms, yet opens
a communications channel to complex machines. In the popular conception, code is
associated with digital computing only. We are, in this article, attempting to correct
both the historical elision that led to the misconception that only digital platforms
are coded systems.
The first modern electronic analog computer, the special purpose “Polyphemus,” was
invented in 1938 by George Philbrick, then refined into general purpose versions in
Germany and the USA during World War II (Holst 1982, 144) (Ulmann 2019, 1763). Electronic
analog computers use electricity as an “analog” or dynamic model of real world systems
being studied (such as planetary motion, economic behavior, stresses on bridges, and
the aerodynamic performance of aircraft designs). As one popular guide to analog
computing from 1952 puts it:
In these devices physical quantities, such as voltages and shaft rotations, are made
to obey mathematical relations comparable to those of the original problem. The physical
quantities, or machine variables, which may be conveniently varied and measured in
the laboratory, must, then, behave in a manner analogous to that of the original variables.”
(Korn and Korn 1952, 2)
In the case of electronic analog computers, electricity itself was the analogous substrate
employed. Users would program the computers to mimic the behaviors of the systems
they wished to study and then input variables to compute how the system would behave.
Until about 1970, analog computers were significantly cheaper, smaller, and faster
than digital computers and saw widespread use in business, government, and universities
(Korn and Korn 1952, 2) (Gilliland 1967, 1-1). We’ll explore the analog computer
further in the following sections as we follow Volleyball’s code up to higher and
higher levels of abstraction. First, however, we must take a look at the Odyssey,
which we will regard as a special purpose electronic analog computer.
The Odyssey’s prototypes were developed by a team of engineers led by Ralph Baer at
U.S. defense contractor Sanders Associates from 1966 to 1969 (Baer 2005). Because
the console was designed to play real-time interactive games and remain inexpensive
enough to be released as a consumer product, the use of analog computing circuitry
was a logical choice: not only were the engineers at Sanders extremely familiar with
such implementations, but analog computers’ speed of operation suited the real-time
gameplay that Baer desired.[7] Baer’s “TV Games” console, however, would be custom built to dramatically reduce
the cost and complexity of the device, eliminating all circuitry that didn’t serve
to enable the suite of games imagined by its engineering team. Nonetheless, despite
its limited internal circuitry, the Odyssey prototypes retained a high degree of user
programmability via a bank of switches that served to re-route the internal circuits
to produce many different possible machine states, or analogs of physical behavior.
Magnavox engineers, as they refined the design from 1970 to 1972, replaced this interface
with a card-based system. Programs were pre-manufactured into circuit board based
“game cards” that were then inserted into a slot in the console. Each card contained
44 pins that could be interconnected in numerous different ways. Thus, the end user
need only insert the proper numbered card to load a particular program. This design
proved highly influential in the home console industry that the Odyssey spawned.
The game Volleyball that we are analyzing here used game card #7 (Figure 2).
Figure 2: Game card #7. Photograph by Zachary Horton
Internal Odyssey circuitry uses a nominally 5.6V single ended power supply. Its circuitry
is organized into ten modules (circuit boards) that take the form of removable “daughter”
cards plugged into slots on the Odyssey motherboard. Signals are passed from daughter
card to daughter card in a variety of ways including analog and digital signals. The
motherboard mostly consists of direct connections between daughter cards. However,
it also contains circuitry for adjusting spot size, wall size, ball speed, a latch
circuit (“crowbar”), and an RF modulator to encode its video signal into the format
required by consumer televisions of the period. In Level 2, we will discuss specific
sub-circuits within the Odyssey and the differential equations that describe them.
In today’s digital computers, electrical components on motherboards are used to condition
electrical current to power various devices (from processors to amplifiers to LCD
arrays) or to carry digital signals from one processor or memory bank to another.
In analog computers, electrical components become the processors themselves: by altering
the current or voltage of electricity within their circuits over time, they alter
the information contained in those flows. Each banal electrical component, then, becomes
an information processor analogous to a line in an equation or a digital programming
language. Let’s take a look at several common components.
Resistors reduce the available voltage by converting some of the available power into
heat. They follow Ohm’s law, which states that the current through the device increases
linearly with the voltage across it as determined by the device’s resistance (Horowitz
and Winfield 2015, 4). Due to their extraordinarily linear behavior, they can predictably
convert certain states to others, and are particularly useful for creating relationships
between multiple time-varying voltage and current sources. A particularly interesting
case is potentiometers which are resistors whose resistance can be internally changed
by rotating a physical mechanism. As we will see below, potentiometers enable user
input in the form of rotating knobs.
Capacitors follow a different type of model which has a time dependence. In capacitors,
the rate of charge (voltage increase) increases linearly with the current through
the capacitor. The ratio is determined by the device's capacitance (Horowitz and Winfield
2015, 19). Thus, capacitors can act as timers, producing repeatable change over time
as they charge or dissipate.
Diodes have substantially different behavior than resistors and capacitors because
the current through the device is affected by the direction of the voltage across
it. A diode can be thought of as a one-way valve for current with a minimum voltage
required to “push” the valve open (Horowitz and Winfield 2015, 31). In reality, the
equation governing the relation between voltage and current in a diode is very complex.
We will use a piecewise linear model that combines the Constant-Voltage-Drop Model
with the Small-Signal model for the discussions in Level 2 (Sedra and Smith 2015,
190-200).
The last component we consider in this article is the transistor, which can be thought
of as an electrical switch, similar to the spigot of a garden hose. It is a three-terminal
device, where one terminal (called the base), allows turning “on” and “off” the flow
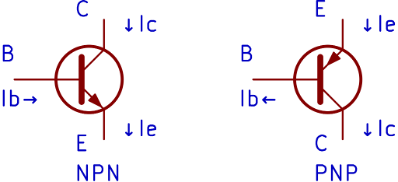
of current between the two other terminals (collector and emitter). The Odyssey uses
NPN and PNP Bipolar Junction Transistors (BJT). BJT’s are current controlled devices,
meaning the current through their “base” terminal determines how much current can
flow through their collector and emitter terminals. In Figure 3, we show the symbols
for the NPN and PNP transistor as well as the directions of current through the “positive”
terminals (Horowitz and Winfield 2015, 71 76)..
Figure 3: (Left) A NPN Transistor with collector, base, and emitter pins labeled with
arrows indicating positive current direction. (Right) A PNP transistor with equivalent
labels.
Figure 4: Odyssey schematic from the Odyssey service manual (Magnavox 1974)
The motherboard hosts ten daughter cards. There are four spot generators (ball, wall,
player 1, player 2), one summer, one “gate matrix”, one horizontal sync generator,
one vertical sync generator, and two flip-flops (Figure 4). Each of these daughter
cards is constructed using a combination of the basic electrical components detailed
above. For example, the sync generators use capacitors to produce regular timed signals
to sync with televisions, the flip-flop uses transistors to switch between two possible
states (directions the in-game ball can travel), the spot generators use transistors
to draw the vertical and horizontal boundaries of player avatars, a ball, and/or a
wall, and the summer uses a series of diodes to combine these various shapes into
a single video signal. The motherboard has one forty-four pin edge connector which
accepts the “game card.” All game cards consist solely of physical connections between
the forty-four pins. The simplest example is a connection from pins two to four which
provides power from the batteries or wall jack to the internal circuitry of the Odyssey.
This function harnesses the analog nature of the console to both power up the machine
and start the game program simultaneously. The motherboard has two twelve-pin Molex
connectors for two controllers. The notable parts inside each controller are three
three-terminal potentiometers and one three-pole,[8] double-throw pushbutton switch.
The game card for Volleyball engages the following functions (Figure 5):
| Pin Connections | Function enabled |
| 2-4 | Connect supply voltage to 5.6V regulator input (power all circuitry) |
| 6-8-10-14-16-20-22 | Supply 5.6V to Player 1, Wall, Ball, Wall Shorten Resistor, Wall Widen Resistor. Power gate matrix output resistors. |
| 13-27 | Connect ball-wall contact signal to crowbar input (motherboard latch) (setting the conditions under which the ball disappears). |
| 23-25 | Connect crowbar active signal to ball disable (causing the ball to disappear when the above condition is met). |
| 30-34 | Flip-flop bidirectional resistor output to ball horizontal direction |
| 31-39 | Player 2 on screen to gate matrix player 2 input |
| 35-37 | Player 1 on screen to gate matrix player 1 input |
| 42-44 | Put resistors in parallel to increase ball vertical response speed |
Table 1.
Figure 5: Table of Volleyball game card’s (#7) connections and functions.
At the hardware level, this is how Volleyball works: The game card “switches on”
four spot generators, each of which produces an on-screen element: two square “players”
(simulated volleyball players), one vertical “net” in the center of the screen, one
small “ball,” and a resistor that changes the vertical timing of the wall-spot generator
so that the normally infinite height “wall” spot is shortened so it resembles a “net”.
The ball’s horizontal and vertical positions are controlled by the charge in two respective
capacitors. The charge of the vertical position capacitor is set by the “English”
potentiometer (which appears to players as the “English” knobs on their controllers)
of the most recent player to make contact with the ball. The charge of the horizontal
position capacitor decreases or increases based on the flip-flop’s state, propelling
the ball signal horizontally across the screen. At the same time, the gate matrix
continuously monitors the ball, wall, and player signals from their respective spot
generators. If any two are “on” at the same time during the electron beam’s scanning
of the TV screen (represented internally by the Odyssey’s oscillators that produce
the NTSC timing signals), then the two objects have made contact on the screen. When
the gate matrix detects such contact between a player and the ball, it sets or resets
the flip-flop in order to change the direction of the ball’s horizontal travel and
transfer control of vertical position to the correct English potentiometer (player
controller).
This process, by which a collision between the ball and an on-screen player is detected
and causes the ball to “bounce” in the opposite direction, is a perfect illustration
of the conjoining of the digital and analog in the Odyssey’s logic. The electrical
charge stored and dissipated in the horizontal position capacitor is a purely analog
phenomenon, like water splashed into or draining out of a tidepool. This propels the
ball along the screen. But at the same time, the position of the flip-flop circuit
is binary: it is in either one state or the other (depending on the particular state
of its transistors), and that state determines whence the ball flies. Thus, digital
states are manifested in continuous physical properties within the console.
The summer daughter card combines the signals of the four different onscreen “spots,”
passes this “composite” signal to the RF modulator daughter card and subsequent RF
filter and the output is sent to a raster scan device (consumer television). Thus,
the console’s video output is not merely the final step after the position of each
graphical frame has been rendered digitally by the system, as it would be with most
graphical outputs today. Here, not only does the Odyssey draw each frame line on
the fly, like the later Atari VCS,[9] but in addition, the gate matrix monitors the spot generators to determine if any
are on simultaneously at a given position of the scanning beam. As we noted above,
this information is used to detect the coincidence of particular elements — such as
when the ball hits a player spot.
The Odyssey contains no circuitry to arrest the movement of the ball before it exits
one side of the screen or the other. This presents a potential problem for a game
meant to simulate the real-world sport of volleyball, in which making contact with
the net causes the ball to drop to the ground (physical event) and exit play (logical
event). However, Volleyball simulates these events through the implementation of
a “crowbar” circuit located on the motherboard, routing the ball’s signal through
its output terminal. The crowbar, physically constructed from a thyristor, is best
described as a latch (Horowitz and Winfield 2015, 208). During normal operation the
crowbar is off. When a signal pulse is received on the crowbar’s input port it activates
and connects its output pin to ground. The crowbar then uses the current flowing through
it (from the [10]output terminal to the ground) to keep itself active (and the output almost shorted
to ground) indefinitely. To bring the crowbar back to the inactive state, the current
flowing from output terminal to ground must be interrupted. The crowbar reset circuitry
(hardwired to the Reset button on the Odyssey’s controllers) accomplishes this by
shorting the current away from the crowbar’s output to ground along an alternate path.
Without current flowing through it, the crowbar becomes inactive due to lack of electrical
energy. In Volleyball, Game Card #7 connects the input and output of the crowbar circuit
such that coincidence between the ball and wall (“net”) spots activates the crowbar,
which then renders the ball invisible by shorting the ball’s active signal to ground.
Momentarily, pressing either controller’s Reset button resets the crowbar (rendering
the ball visible again). Additionally, the losing player’s Reset button flips the
flip-flop to its opposite state, thus resuming the program and sending the ball flying
back onto the screen.
The moment the ball makes contact with the net, then, it seems to the players to disappear
from the screen, simulating arrested movement (the physical event of a volleyball
hitting a net). At the hardware level, however, the ball’s signal is still present
— it has been pulled low by the crowbar circuit but not all the way to ground (0V).
Thus, its signal possesses enough voltage to trigger the flip-flop but not enough
to enable the ball’s signal to be added to the console’s output (television) signal
via the summer daughter card. To the user, it appears as if the ball has been eliminated,
but in actuality it is still invisibly bouncing back and forth until it misses one
of the player spots and finally exits the screen. As we will discuss in Level 4,
the logical event of halted play must be enacted by players (prompted by the phenomenological
event of the ball becoming invisible) since it isn’t enforced by the console’s logic.
This invisible ball is a pseudo end-state to the program: it is technically still
running on the hardware, but appears to the players to have stopped, awaiting their
input (the next serve). Thus, the “netted” ball is something of a ghost, actively
haunting the system even after the players believe it to have expired.
The Odyssey’s designers felt that this was an adequate physical approximation of a
game-stopping consequence (as we’ll discuss further at the subsequent levels) that
could be coded without undue expense or complexity. It is an example of hardware
economizing combined with creative programming: in Volleyball the crowbar function
is used to simulate the ball hitting the net; whereas, in other games the crowbar
is programmed to simulate a torpedo hitting a ship (Submarine), an airplane being
shot out of the sky (Dogfight), a cat catching (and presumably eating) a mouse (Cat
and Mouse), or a spaceship burning up in the sun (Interplanetary Voyage). These conditions
have very different meanings to players in their different contexts, even if they
all arise from the same hardware function, programmed differently. We will need to
look at higher levels of this code to trace out the process by which hardware states
are transformed into symbolic meaning, but already we have seen that in analog computing,
the hardware layer is a direct substrate for programming. Rearranging or reconnecting
components in different configurations produces different electrical behavior, enabling
new sets of interactions, input, and output. While this is clearly a continuous —
that is, analog — process of altering current and voltage over time, it is not true
that the analog and the digital cannot coexist. The crowbar, the gate matrix, and
the flip-flop subcircuits all utilize continuous flows to encode digital logic in
definite states (invisibility, coincidence, and direction, respectively). Fully discrete
hardware (i.e., digital processors) is not required to implement digital logic because
digital logic can directly interface with analog signals. It may come as a surprise
that the two can coexist quite productively in the Odyssey. However, this is what
historically enabled the decades-long practice of analog computing.
It is commonplace that higher levels of code (from machine to assembly to language
to scripting, for example) are always more abstract than lower levels of code (Abelson
and Sussman 1996, 491-610). As we’ll argue, however, this is not necessarily the
case in our example: hardware capabilities can reach high levels of abstraction (as
the crowbar example shows); however, higher levels are not necessarily more abstract
than the hardware level. A great deal of Volleyball’s program is coded directly at
the hardware level: game card #7 connects the inputs and outputs of the circuits we
have described, producing these effects. This does not mean, however, that there
are no higher levels of code. After all, what we have described so far is primarily
the movement of electrons through circuits. Higher levels of this codified system,
each of which represents a different way to characterize Volleyball’s code, were used
to program the game, and can be uncovered again through reverse engineering in order
to reveal much more about the game’s nature, how it functions, and what its programming
assumed about its players.
Level 2: Mathematical Operations
In order to understand the formal relationship between hardware platform (Level 1,
above) and logic flow (Level 3, below), we must explore the relation of each to mathematical
formulae. This is the secret to the historical success of the electronic analog computer.
These computers were not only used to model physical phenomena to aid in the design
of everything from aircraft to atomic reactors but also to solve equations that would
be far too time consuming to solve manually or via digital computers of the time.
As Granino Korn noted in 1962, “Unlike digital computers, most analog computers employ
distinct computing elements for each mathematical operation required to solve a given
problem (parallel operation). Parallel operation is an essential reason for the very
high computing speeds possible with d-c analog computers” (Huskey and Korn 1962, 1-4),
(emphasis in original). Put simply, analog computers could perform, at very low levels
of abstraction, many mathematical equations directly. Digital computers, by contrast,
could only sequentially perform a fixed set of operations, usually limited to addition
and subtraction (Brown and Vranesic 2009, 249-295). Thus, in digital computers, hgher
order operations had to be built up from these lower level ones, necessitating higher
levels of software abstraction. In contrast,analog computers could perform calculus
directly at the hardware level (Korn and Korn 1952, 8).
A complete mathematical formulation of Volleyball would serve as a legitimate low
level expression of its code, but it would require many pages of this journal. Thus
we will only undertake a complete description of the code at a higher level (Level
3). In this section, we will examine the relationship between hardware and logic
to demonstrate, for two of Volleyball’s functions, how code can be expressed as mathematics
that blend continuous time, continuous values, and discrete meaning.
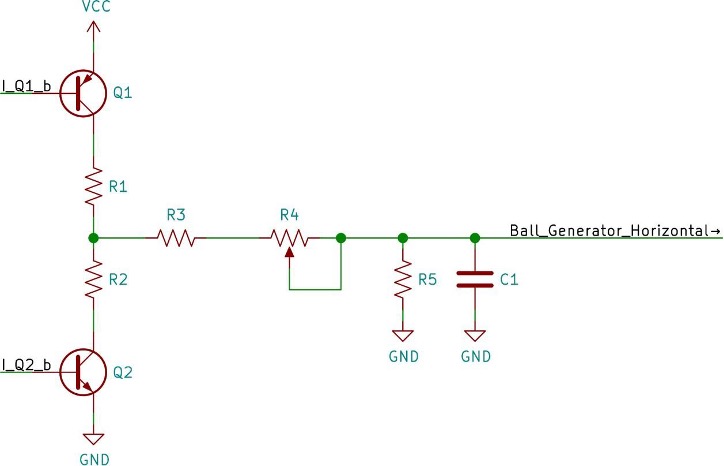
The first example we consider is the regulation of the ball’s horizontal position
by an “integration” circuit in Volleyball (Figure 6). On the left are two transistors
that are part of the flip-flop that tracks the direction of the ball. Their output
is the “direction” that charges or discharges the horizontal position capacitor.
Figure 6: The sub-circuit in Volleyball which controls the horizontal position of
the ball. The voltage at “Ball_Generator_Horizontal” determines the ball’s horizontal
position.
In Figure 6, the voltage between node Ball_Generator_Horizontal (abbreviated Vb) and
ground defines the horizontal position of the ball. Lower voltage means the ball is
further to the right of the screen. Because this differential equation describes a
continuously variable function, there are an infinite number of possible ball positions
described by this equation and instantiated during the running of the Volleyball program.
This is strongly in contrast with digital systems that can only support quantized
positions on the screen
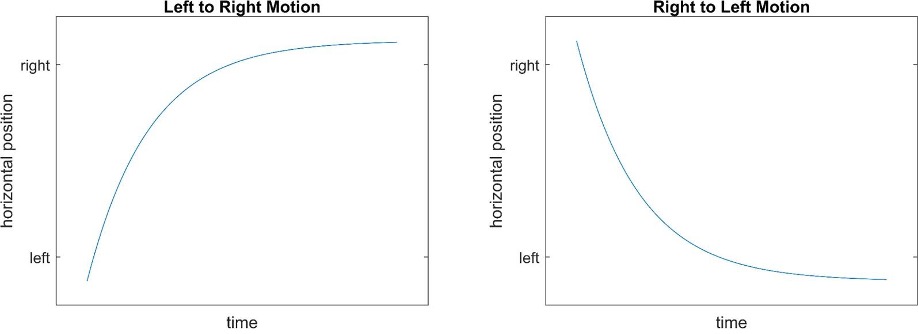
The flip-flop has two states, “left motion” and “right motion.” In the configuration
shown in Figure 6, the transistors are complementary, meaning if one is off, the other
is on. In the “right motion” state, the base of Q1 has a high voltage comparable to
its collector, meaning that a current flows through its base pin that is too small
to turn it on. Meanwhile, Q2 has voltage higher than its emitter applied to its base,
great enough that the current through it’s base pin turns it on. Using Kirchoff’s
Voltage Law (KVL) and Kirchoff’s Current Law (KCL)[11], we can write a differential equation for the voltage at Vb for the case of “right
motion.”
Assuming the initial position is beyond the left side of the screen (Vb is a high
voltage like Vcc) then the equation above has the solution (Tenenbaum and Pollard
1985).
In the case of “left motion” starting from beyond the right side of the screen (Vb
is a low voltage like 0) then the solution looks different, but is qualitatively the
same as shown in Figure 7.
Figure 7: (Left) The general shape of Vb(t) for left to right motion. (Right) The
general shape of Vb(t) for right to left motion.
In general, the solution to a differential equation cannot be expressed as an easily
evaluated equation (closed form), as was done for Vb above. When available, such solutions
instantly provide a qualitative description of a systems behavior in all conditions
and are thus very useful for designing a circuit’s behavior. In this example, such
a solution was only available because the transistors were assumed to be in a particular
operating mode which rendered the considered circuitry linear. While more complicated,
nonlinear differential equations can be characterized using simulation or advanced
techniques from dynamical systems theory (Khalil 2002). using such techniques to qualitatively
describe a system as large as the Odyssey would be an incredibly difficult and labor
intensive[12]. Thankfully, individual sub-circuits can be described qualitatively and “sending”
sub-circuit terminals can be connected to “receiving” sub-circuit terminals without
greatly affecting the “senders” behavior. This property makes it possible for the
analog programmer to design behaviors without considering the entire circuit at once.
In the extreme case, it makes the abstractions later described in Level 3 possible.
This illustrates the complexity and nonlinearity of analog systems.
When used as substrates for computing, these dynamic systems can be harnessed to form
analogs of other complex, nonlinear systems; this was the principle insight that lead
to the field of analog computing. Digital systems, by contrast, are necessarily simplified
models of complex systems, built up through code from simpler to more complex forms.
Put another way, digital computing at this level — which we might call assembly code
— must combine low-level hardware states (binary) into more complex mathematical functions.
To cause a ball to accelerate across the screen, as in this example, the code must
combine many simple arithmetical functions into a differential equation, then apply
that equation to a pre-defined grid [13]of positions to move the ball across the screen from pixel to pixel. The analog computer,
as we have seen, begins with a differential equation that simply describes the physical
behavior of electrons within the circuit. Then, while the digital system must somehow
simplify the equation it has built up, approximating positions within limited matrices,
the analog computer simply feeds its signal into an analog output. The granularity
may get reduced by the output device (the phosphor pattern on a CRT television, for
instance), but such resolution reduction is not part of the machine’s code[14].
The analog computer converts physical states into symbolic or logical ones through
equations that describe that physical behavior, while the digital computer begins
with simple data, then must build up ever more complex instruction sets to construct
a set of equations to transform that data into results that can be output. In the
analog computer, dynamic states are translated into the symbolic, while in the digital
computer, the symbolic is constructed piecemeal, always under conditions of simplification
and approximation.
At the next level we will examine some of the implications of this difference for
the programmer. First, however, we’ll look at one more example of the Odyssey’s physical
states translated into a symbolic (mathematical) model: the gate matrix’s detection
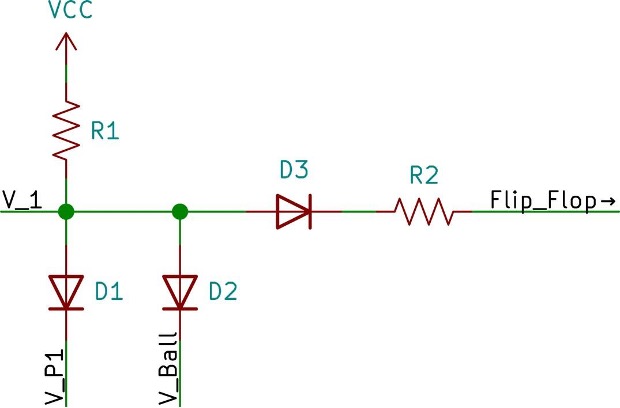
of player and ball contact. The sub-circuit considered is shown in Figure 8.
Figure 8: Subset of Odyssey circuitry that detects contact between a ball and a player.
We can view the circuit as mapping the two inputs (VP1, VBall) to one output (Flip_Flop).
The line VP1 has a high voltage, close to Vcc, when the Player 1 spot is being drawn
on the screen. The same applies to the VBall input. Meanwhile, the output is connected
to the flip-flop that controls the directional motion of the ball. Current through
R2 triggers the flip-flop and changes the direction of horizontal travel of the ball.
Using the circuit laws and models mentioned thus far, the equation for IR2 as a function
of VP1 and VBall can be expressed in piecewise linear form.
In order to simplify this equation, we have to consider the four possible different
cases encompassing all the possible combinations of the voltages on VP1 and VBall.
| VP1 | VBall | ID1 | ID2 | V1 |
| 0 | 0 | ~0.5*(Vcc - Vthr)/R1 | ~0.5*(Vcc - Vthr)/R1 | ~Vthr |
| Vcc | 0 | 0 | ~(Vcc - Vthr)/R1 | ~Vthr |
| 0 | Vcc | ~(Vcc - Vthr)/R1 | 0 | ~Vthr |
| Vcc | Vcc | 0 | 0 | Vcc - IR2R1 |
Table 2.
Figure 9: Table of solutions for ID1, ID2, and V1 given all possible combinations
of VP1 and VBall.
Thus, across the four possible combinations of VP1 and VBall , V1 there are two possible
output values. With this observation, we can write down a simpler expression for IR2.
In essence, the diodes perform an AND operation between VP1 or VBall and send the
detection of coincidence to the flip-flop.
These equations describe a system of interactions that incorporate both continuous
(analog) functions and discrete (digital) ones. A continuously variable function
(ball position in time) acts on a threshold equation to determine two binary states:
the coincidence between a player spot and the ball spot, and the state of the flip-flop,
which determines which of the two directions the ball travels in.
Unlike at the other levels, here we can see that the mathematical operations clearly
specify the behavior of Volleyball’s physical instantiation in hardware. Similar to
assembly code for digital computers, these equations determine the specific states
of physical components — that is, they describe the behavior of physical systems.
However, unlike digital computers, there is almost a one-to-one mapping between physical
states and something perceivable by the player. These equations mix continuous with
discrete, analog and digital. They describe discrete states of the machine, but as
piecewise continuous functions. Thus, at this critical level of transformation between
hardware substrate to abstract logic, there is no definitive move from the analog
to the digital; both are operative simultaneously. What we observed at the hardware
level, then, holds even at the level of translation into the symbolic.
Thus this level is unique in its affordances for the programmer. For example, if the
game designer (programmer) wishes the ball to travel at a particular speed, then the
equations discussed, and specifically the solution to the differential equation, can
guide the choice of resistors and capacitors that accomplish that goal. Mathematical
notation thus provides us with a glimpse of the transitive nature of Volleyball’s
code: it operates upon the material substratum of the console, while remaining symbolically
manipulable by humans at other scales. This is the reason that code can jump from
scale to scale, linking levels together in communicative feedback loops.
Mathematical equations capture an essential aspect of a code’s meaning: the formal
rules by which values are transformed as they pass from one level of abstraction to
another. These are passage points where code can intervene in scalar transformations.
We typically think of mathematics in code as primarily attempting to capture something
about the analog world (encoding the continuous into the discrete) or performing calculations
on other stored numbers. In this case, however, our glimpse at Volleyball’s underlying
equations reveal an intricate entanglement of analog and digital functions that together
describe the simplest of on-screen transformations in the program: bouncing the ball
back and forth across the screen. Here there can be no delineated point at which the
analog (phosphors on the screen, current in circuits) has been transformed into the
digital, a threshold beyond which all coded manipulations are in a simulated, digital
world. Rather, analog and digital functions rely upon each other and are interwoven.
The mathematical components of code exert control over the system, but the system
cannot be thought of as a mere simulation of the real. We could not claim that the
ball in Volleyball is definitively digital or definitively analog. Rather, it appears
to bounce between the two.
In this sense the ball in Volleyball is a unique object in early gaming and early
programming, and serves as an icon or mark of transitivity: it moves of its own accord
(according to the equations we’ve related here); it can be made to bounce, to halt,
to disappear, to soar, or slam downward like a missile.[15] The ball is a boundary object that can bounce between levels of abstraction, as
both an object operated upon by code and as code operating on its various environments.
These sorts of liminal coded objects are rarely considered as such, but perhaps that
is because the equivalent level at which they can be resolved, assembly, itself receives
little attention. Still, we could look to other boundary objects like wavetable synthesis,
scanners, and quartz oscillators as ubiquitous digital equivalents.
The liminal quality of Volleyball’s ball provides an interesting response to Kittler.
Because the ball is both analog and digital, material and codeable, we can accept
Kittler’s argument that continuous or analog structures are more characteristic of
the physical world as a whole while rejecting his assumption that they are “unprogrammable.”
That is, we can accept his argument that digital systems capture or represent only
a small slice of the world and obscure even that through symbolic abstraction but
also reject his dichotomy between continuous and programmable. Volleyball’s ball
demonstrates that continuous structures are very much programmable, and that code
and continuous material substrate can sustain reciprocal, non-reductive relations.
Let’s follow this analog-digital hybrid volleyball on its path as it weaves together
multiple scales, multiple procedures, and multiple bodies.
Level 3: Abstract Logic
When programmers write code and humanities scholars read it, the code encountered
is usually expressed in a high-level programming language. These languages are powerful
because they retain the precision and machine readability of lower levels of code
and at least some of the features of natural language. That is, they use words and
syntax borrowed from natural languages (usually English) wherever possible to aid
in the composition and human readability of the coded program. Code written in a
programming language is semantically unique in that it is addressed to two audiences:
machines and humans.
Programming languages are not available for analog coding. This is because the machine
is an analog of a physical system, not a linguistic one. While any analog program
can be approximately described in natural language (as we have attempted thus far),
there is no necessary connection between sequences of machine instructions and linguistic
sequences that would render language a particularly suitable form for coding analog
machines. Historically, analog computer programmers tended to use a semi-standardized
block diagram notation system to record, check, and disseminate their programs. Similar
to digital programming languages, block diagramming standardized code so that it could
be “set up” (analogous to compiling) on different architectures and understood by
different human programmers. Additionally, the diagrams served as a record of the
code fed to the machine, just as today source code is sharable, archivable, and readable
outside of its particular expression when run on its intended platform.
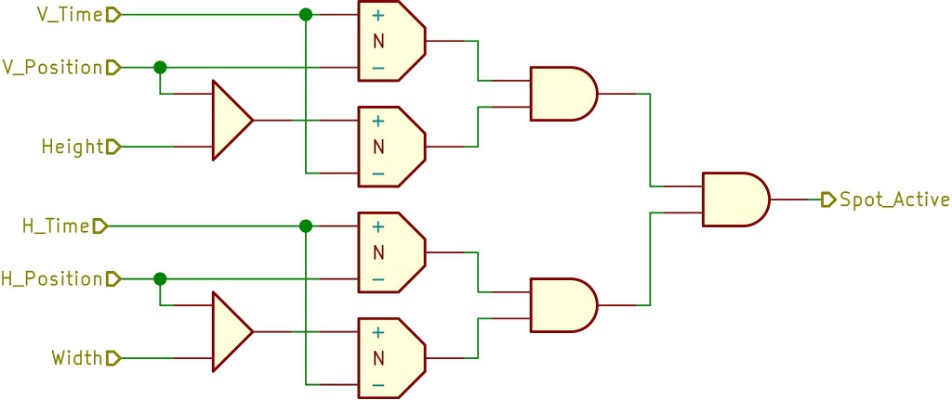
Block diagramming essentially visualizes the logical flow of a program. Each block
simultaneously represents a logical operation and a hardware component. Figure 10
includes nine basic programming blocks closely adapted from the Handbook of Analog
Computation (Gilliland 1967). These are the building blocks of Volleyball’s code.
Figure 10: Each of the nine program blocks used in the Volleyball program and a basic
explanation of their inputs (left sides) and outputs (right sides). “&&” and “||”
represent the logical AND and OR operators respectively.
These program blocks make intuitive sense to the programmer, and also convey precise
instructions to the machine. To recall our previous example, IF the ball makes contact
with the net, THEN it will disappear. Using program blocks, this could be represented
using an AND block to detect coincidence between the ball and the wall and flip-flops
which latch upon receipt of the AND gate’s output in order to make the ball disappear
for the remainder of the program. Every logical operation that comprises a program
can be diagrammed in this fashion. Volleyball is simple enough to have been programmed
entirely in its coders’ heads and therefore Ralph Baer and his collaborators may never
have developed a formal block diagram when designing its logic. Nevertheless, it is
quite possible to reverse engineer the program and formally express it as code, as
we have done in Figure 11.
Figure 11: Full Volleyball program code, expressed in analog programming block notation.
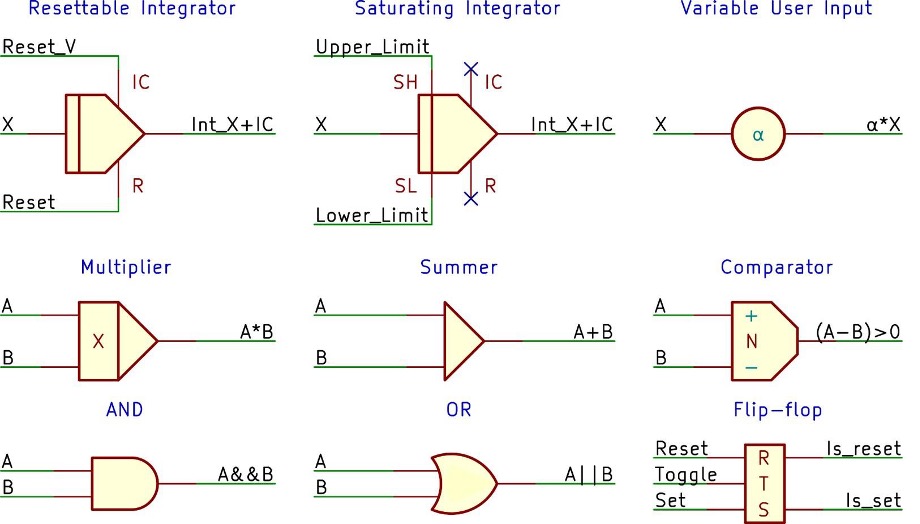
The spot generators indicated in Figure 11 have the following logical structure (Figure
12):
Figure 12: The spot generator sub-circuit is repeated for both players, the ball,
and the wall.
Notating Volleyball in this way reveals a different aspect of the same code we have
explored as hardware and as a series of mathematical equations. Here we notate not
the electrical components, nor a mathematical representation of voltage transformations,
but rather the more abstract level of logical flow. When viewing the diagram as a
whole, Volleyball’s larger-scale relational structure is revealed. We may notice,
for example, the centrality of the ball: it is acted upon directly by the players
via their controllers but also subject to a number of conditional branches that govern
its state. As players of the game, we might expect that our avatars, the player spots,
are the most central objects in the program. However, this logical flow diagram alerts
us to the fact that they primarily serve as input to other processes — that is, as
triggers. Very little affects them, while they affect the logical flow in a number
of ways.
From a gameplay standpoint, this produces an interactive system that does not render
its playable characters vulnerable to in-game threats: these avatars have free reign
in the world of Volleyball. They primarily act to constrain their principal medium
of exchange: the ball. On the face of it this isn’t surprising: sports games are
usually more about doing things to a ball than avoiding or mitigating pitfalls directed
at your avatar. However, even in this genre of game, avatars in most sports games
are highly constrained by coded conditional branches. For example, we are not aware
of a later volleyball video game that allows its characters to cross over to the other
side of the net during play. The same sort of conditional branch that causes the
ball in Volleyball to become invisible when it makes contact with the net typically
halts player movement. No such conditional branch is present in the above program,
and sure enough, players can move their avatars over to their opponents’ side of the
court. They can even leave the court entirely! Thus the logical structure of Volleyball
enacts a particular form of player agency.
Granino and Theresa Korn, in their classic 1952 text on analog programming, take pains
to describe the creativity involved in designing any particular analog computer program:
There are usually many possible setups (programs) for a given problem. It will always
be somewhat of an art to find the setup which will result in the greatest possible
accuracy or in the most economical use of the computing elements. Experience as well
as ingenuity will give the operator a feeling for the new mathematical medium, and
one may say that an elegant setup will be aesthetically satisfying as well as practically
useful. (Korn and Korn 1952, 22)
Today’s programmers will recognize and relate to the concept of elegant coding: while
there is no single “right” way to achieve particular results from code, there are
various more or less elegant ways to do so through concision, recursion, and creativity.
As Mark Marino notes, “people who do not program often assume that code is like arithmetic,
with symbols and processes that are expressed in the only way possible. However, programming
actually creates artifacts of processes that reflect the selections made by the programmer
from the paradigm of possible options” (Pressman, Marino, and Douglass 2015, 29).
In the case of Volleyball, these functions could have been implemented in a number
of different ways. What is perhaps most striking is the economy of this program:
it makes use of the absolute minimum number of conditional branches and drawn elements
necessary to simulate a game of volleyball. It is working within the hardware limitations
of its platform, but as one of the core games written during prototype development,
it also influenced those hardware specifications. For example, an extra resistor
and its attendant parallel wiring and connection to the game card edge connector had
to be added to the motherboard in order to implement the program block we have designated
as “Wall Vertical Height Selection” above. This is the function that limits the height
of the Wall spot in order to refashion it into a short volleyball net. Out of twenty-eight
commercially released Odyssey games, only Volleyball actually calls this function
(via a trace on game card #7).
Another feature linking hardware with logic flow that is revealed by block program
notation is the vertical and horizontal timing sources built from self-resetting integrators.
Together, the analog output of these circuits represent the X-Y position of the television’s
electron beam and thus sets the timing for the entire program. It is remarkable that
this sense of time is accomplished purely using program blocks. In digital computers
this is not possible, since time is discrete, and must be incremented by some external
source such as a crystal oscillator (Heiserman 1978, 14) (Patterson and Hennessey
2014, 33). Here, by contrast, the bidirectional coupling of analog and digital elements
in the program, their mutual permeability, enable digital events to occur in continuous
time.
Like most code, Volleyball mediates between human-readable accounts of the world and
machine-readable models of non-ambiguous instruction. Annette Vee describes this
dual function of programming compositionally as “the constellation of abilities to
break a complex process down into small procedures and then express — or ‘write’ —
those procedures using the technology of code that may be ‘read’ by a nonhuman entity
such as a computer. To write code, a person must be able to express a process in
hyper-explicit terms and procedures that can be evaluated by recourse to explicit
logic rules” (Vee 2017, 22). While Vee compares the machine-logic structure of code
with its linguistic properties, our block programming notation is primarily visual
and networked rather than linguistically expressed. Does this help (or compel) us
to conceive of the human-readable layer of code, or indeed its composition, differently?
Visualizing logical flow privileges particular machine actions and opens up spaces
for inputs and outputs at other levels of abstraction. This is the level at which
we can study code for its syntactic qualities and topological structures (especially
loops). We can look for linearity or circularity, openings for inputs and opportunities
for outputs. It is the level at which potential is closed and captured for particular
logical structures.
Another characteristic of Volleyball that is far less apparent at the hardware or
mathematical levels, but which is readily revealed by its programming block diagram,
is the precariousness of its main loop structure. Video game programs typically require
a program loop that continually reads input states, calculates trajectories, tracks
progress, remembers inventory and score, and draws the onscreen graphics and sends
them to a frame buffer (LaMothe 1995, 34-43). If the program loop is interrupted
(by someone yanking the power plug out of the wall, for instance), the current state
is lost and the program must start over from the beginning (though it may re-load
saved data). In Volleyball’s program logic, certain timed input pulses continue indefinitely
and the positions of any spots are continuously drawn, but all of the interactive
logic of the game relies on a loop created by successive flip-flop activations. If
a flip-flop is not activated within a particular period of time, the loop terminates.
Player spots are still drawn, but no interaction is possible. To the players, the
game has become inert. No set of computational instructions necessarily repeats as
a result of Volleyball’s logical structure.
If Wilfried Hou Je Bek is right that we should “regard the loop as a species of tool
for thinking about and dealing with problems of a certain nature” (Hou Je Bek 2008,
180) then Volleyball’s contingent loop is a telling detail in the conceptual flow
of this game. In practice, the “volley” in the game’s title refers to a sustained,
repetitive sequence of a ball bouncing off the left and right players. But as we can
readily see, this sequence can’t repeat without direct player input via the controllers.
Our program block diagram reveals that there is no loop connecting an internal signal
to the “Player 1 Position” composite block in Figure 11. In this sense, Volleyball
has a limited runtime without active input. The code will have run its course once
the ball exits the screen and only uninteresting periodic behavior will be produced
by the system, driven by the oscillations of the vertical and horizontal time sources.
In essence, if no player intervenes, the program grinds to a halt. The ball will
not be returned from off the screen, and will not be automatically served. No demonstration
sequence or player prompt will load. In Alexander Galloway’s useful conceptual schema,
Volleyball does not include in its program loop what Alexander Galloway calls “ambiance
acts,” or diegetic actions performed by the machine without operator input (Galloway
2006, 10). The program will have halted until a player presses their Reset button,
which begins the program again. Volleyball’s loop structure represents a way of thinking
about code-mediated interaction as a player loop. Rather than external players merely
triggering timed inputs that modify the specific expressive details of the program
loop, which is otherwise internally consistent and self-sufficient, here the loop
requires the analog world in two-way participation. This program loops through physical
space rather than treating physical space a mere input to be encoded.
This radical form of programming helped to usher in an entirely new form of human-computer
interaction: the video game.
Level 4: Game
In order for Volleyball to be fully playable, its program logic must be supplemented
with another, higher level of code that allows it to cohere as a particular type of
program: a game. At this level, the user is included as part of the program, and its
larger operational context comes into view. For a program that is meant to be a game,
this is the level at which it can be played.
Typically, when analyzing digital code, the user can be bracketed out of the discussion,
assumed as a given, but at a higher level of abstraction than code itself. As Montfort
et al. note, critical code studies is methodologically located in between the scales
of platform studies (underlying hardware) and software studies (processes, users,
and cultural context), even if these scales and approaches tend to blend together
in scholarly work (Montfort et al. 2012, 7). But once again, Volleyball and the Odyssey
confound even the fuzzy distinctions between these levels. Just as the code makes
no sense without reference to the hardware level (the medium that embodies its logic
and makes it “live”), so too must we confront the fact that the game doesn’t even
become a game, doesn’t become executable, without reference to a higher level of abstraction
that includes human players in a closed circuit with the signal paths we’ve been describing,
as well as natural language rules that are an essential part of the program’s instruction
set. As we shall see, when analyzing Volleyball, it is difficult to make even an
analytical distinction between these scalar levels.
Perhaps the most surprising twist in this game for today’s first-time players is that
the Odyssey doesn’t simulate gravity: the ball is not coded to fall downwards! When
hit by a player, as we have seen, the ball changes direction via a digital flip-flop
and increases its speed through the charging of an analog capacitor, driving it to
the right or left depending on the initial condition before the coincidence of ball
and player. But the ball’s vertical position as it travels is determined by the setting
of a special (third) knob on the player’s controller: the “English” knob. Turning
this knob directs the ball upward or downward. The ball’s upward arc, apogee, and
downward arc, together simulating the effects of gravity, are encoded not by game
card #7, nor any digital or analog logic hardwired into the motherboard, nor by a
differential equation, but rather by two very human-readable sentences on the game’s
instruction sheet: “Each player must use his ENGLISH Control to arch the ball over
the NET and then down into his OPPONENT’S playing court. The ball must be directed
down towards the floor of the court and is not permitted to go off the screen at the
TOP or SIDE” (Magnavox 1972, 1).
The result, as surely as the insertion of a parabolic equation in a line of program
code, is that the ball tends to arc over the net and then drop down to the bottom
of the screen. Such is the power of code.
The “Set Up” section of the same document instructs the player, as the second step,
to “place the VOLLEYBALL Overlay on the screen” (Volleyball 1972, 1). The overlay
in question is a thin, offset-printed sheet of plastic cut to fit the distinct rounded
CRT screens of 1960s and 1970s television sets (Figure 13). All but one of the Odyssey’s
twenty-eight released games uses a similar overlay. These overlays make use of a
mixture of three optical effects: opacity (via a special opaque layer applied to the
back that blocks all onscreen elements when they pass through the coated area), translucency
(via graphics printed on the front of a frosted substrate), and transparency (non-printed
areas on a clear substrate). The entire Volleyball overlay is translucent: on-screen
graphics project through the overlay but pick up the color printed thereon. The yellow
backdrop of the Volleyball overlay tints both the players and ball distinctly yellow,
presumably evoking a beach setting.
Figure 13: Volleyball overlay. Scan by Zachary Horton.
The overlay’s design includes two squares. As the instructions explain, the players
must position their avatars inside these “boxes” for every serve. Here, then, written
rules reference and require the on-screen game logic and resulting luminescent shapes,
as well as the physical overlay, which composites two sets of images (those produced
via the cathode ray tube and those statically printed on the plastic sheet). Both
the algorithm (set of instructions) and the elements necessary to execute it span
across multiple media and modalities: graphical overlay (with optical properties of
reflection and refraction), natural language instructions, coded machine behavior
via game card #7 and the various digital and analog circuits it modifies, and human-generated
input governed by the affordances of the Odyssey controller — including the semantic
affordance of the prominent label for its one and only button: “Reset.”
Pressing a button labeled “Reset” in order to serve a ball induces some cognitive
dissonance. Ralph Baer’s final prototype for what was to become the Odyssey, his
“Brown Box,” labeled its corresponding button “Serve.” The Magnavox team changed
the button’s label (though not its function) to “Reset.” The semantic difference
is stark: to “serve” is to provide service to another person, to provide them with
the ball, and to set a projectile in motion. It is a narrative act, both initiatory
and consequential. To “reset,” on the other hand, is to return to the beginning,
to start over. This is a user action that effects a change of machine state: in this
case, enacts a loop that keeps the program running. Here, then, is the missing link
in the machine code’s loop. It is offloaded to human action, but certainly not decoded
or uncoded: the “Reset” button ensures that the human player is not only physically,
but logically and semantically enrolled into the game’s series of machine actions
as a fundamental element of its program logic. In Alexander Galloway’s typology,
which contrasts machine actions vs. player actions on one axis and diagetic vs. non-diagetic
actions on the other (Galloway 2006), this is an example of a non-diagetic machine
action (loop end state) masquerading as a diagetic machine action (ball out of court),
prompting a diagetic player action (serving the ball) that nonetheless reveals its
non-diagetic nature (restarting the program loop) via the tellingly labeled “Reset”
button. While this tell-tale sign is the most blatant slip of the curtain, it is
characteristic of much of the game’s logic of simulation. Even human vocalization
and memory are drafted as game functions: the players must keep a running tally of
their scores, calling them out and retaining the arithmetical chain until a winner
can be declared.
The Odyssey in general, and Volleyball in particular, can be regarded as exceptionally
economical in its design when, from this angle, we trace the ways that its program
code jumps media and seamlessly meshes them together into a necessarily complete circuit
of coded behavior. The overlay, natural language instructions, mathematical functions,
logical program flow, and individual physical states all work as part of a larger
assemblage to define the bounded system that is the game Volleyball. There is no
redundancy between, for example, the instruction set given to the human players and
the instruction set given to the machine. Not only is gravity offloaded to players
as an aspect of gameplay (governed by formal rules) rather than as a machine-enforced
constant,[16] but scoring too is given over to players to adjudicate and mentally tally. The instruction
sheet explains that where on the overlay the ball exits determines who receives points
or takes the next serve.
Of course, players aren’t forced to follow these rules if they don’t wish to do so.
This represents a significant difference between this distributed, analog-digital
system and purely digital ones: digital code has a finality about it — a way of enforcing
constraints without relying on formal human-addressed rules to do so. As Cathy O’Neil
argues, digital systems and their black-boxed algorithms “define their own reality
and use it to justify their results,” creating feedback loops that foreclose appeal
and tend to perpetuate injustice (O’Neil 2017, 7-11). Lawrence Lessig has made a
similar point about the autocratic nature of code, arguing that it prevents unauthorized
behavior from the beginning, which circumvents a fundamental right of citizens to
a legal process to challenge unjust rules. In programmed systems, “code is law” (Lessig
2006, 5). When the rules are baked into the system they cannot be challenged. Compare
this to Volleyball, which codes no prohibition on where players may or may not move
during the course of the game. The human code dictates that “each player must stay
on his own side of the net,” but the machine code does not enforce this. It is a
rule, but one that can be broken: as we have noted, players can move to their opponents’
sides of the net, and even outside of the visible area on the television screen if
they wish.
This “breaks” the game, of course. Players can probe the edges of the machine logic,
but must adhere to the semantic content of the rules and self-police them or the program
doesn’t work. A reversal of priorities, then: the program requires a higher-level
set of semantic structures in order to function correctly. Human language structures
the logic system, rather than the logic system rigidly determining the sorts of semantic
content that can emerge from play. In one sense, then, Volleyball is rigidly structured
by rules. In another, though, the distribution of those rules across various media
and abstraction levels allows them to be differentially (and creatively) applied,
opening up a new space for experimentation and creative interfacing with the system.
McKenzie Wark has argued that such engagement with games can help players to navigate
and find ways to subvert or break everyday reality, which is increasingly structured
by digital system dynamics and marked by gamification. This technosocial milieu,
which Wark calls “gamespace,” has saturated life itself and transformed it into an
agon that instrumentalizes all action and reifies the values of capital (Wark 2007,
008). In gamespace, literal video games have the potential to reveal the ways that
players’ relationship to reality has been coded: “The game opens a critical gap between
what gamespace promises and what it delivers,” acting as the first step toward dismantling
its ideology and discovering ways to subvert its everyday functions (Wark 2007, 032).
Playing games in this way enables the player to “trifle with the game to understand
the nature of gamespace as world — as the world” (Wark 2007, 021).
If games are simulations — of particular spaces, times, and relations, or of gamespace
as a whole — and analog programs are also simulations or analogs of particular states,
then we must emphasize here that Volleyball troubles the usual relationship between
model and reality. This program is meant to simulate a volleyball court and ball,
and two humans playing its titular sport. In standard computational simulations (including
analog ones), humans tweak variables and observe how the system behaves. In video
games, variables take the form of timed inputs encoded through physical interfaces:
buttons, joysticks, voice commands, gestures, and so on. But while that is still
true for Volleyball, the simulation is less autonomous and less autocratic. That
is, this coded system does not foist the constraints of the simulated reality on the
user and challenge them to perform within those constraints. Here, code is not law,
and the simulated world it conjures is permeable with the reality it simulates. As
we have seen, Volleyball calls its players to a somewhat different challenge: rather
than understanding and mastering this new, coded, virtual reality, the player is tasked
with completing the simulation itself, with closing the gap between model and world,
analog and referent.
The players must add gravity to this simulated beach volleyball game. The players
must keep the program loop going by constantly resetting it (flipping the flip-flop
and recharging the horizontal position capacitor) via their Reset buttons. The players
must enforce their starting positions vis-a-vis the mediation of an overlay that is
not part of the machine code and thus can only be integrated by the human nervous
system. The players must supply the interpretation of various plays to adjudicate
and assign scores. The players must supply the memory to keep track of these scores
and declare a winner. We may read this as a particularly neoliberal enrollment of
human capability into gamespace (not only do the players have to perform within a
simulation, they have to take on the labor of completing the simulation that enslaves
them), or we may read it as something of an inverse of today’s ubiquitous and seamless
gamespace: instead of restructuring (gamifying) the player’s relations with the social
and material world by instrumentalizing and quantifying their actions and enrolling
them in a milieu of perpetual competition, Volleyball asks players to generate their
own bridge from the virtual to the real. In this conception, instead of gaming exposing
the gap between a promised milieu and its actual mechanics, as Wark argues is the
norm today, gaming here represents playing in and exploring the gap itself, in the
notable absence of teleology or promises.
One of us, Zachary Horton, often teaches the Odyssey platform in his undergraduate
courses and has witnessed many students struggle with Volleyball in particular. Players
must use three different knobs and one button nearly simultaneously to keep the program
running (Figure 14). While it is not unusual for games or other software to require
difficult, coordinated patterns of movement (this is notoriously endemic to the street
fighting genre of video games, for example), these functions are usually tied to avatar
or user actions rather than the layer of simulation itself.
Figure 14: Odyssey controller. Photograph by Zachary Horton.
While controlling multiple continuously variable processes with only two hands is
indeed difficult for most players, the true challenge of this game is, we hypothesize,
due less to poor hand-eye coordination than it is to the conceptual leap, unfamiliar
to today’s gamers, from inhabiting an immersive simulation to completing and maintaining
it. Roughly speaking, the conceptual leap in the mentality of the player is equivalent
to the conceptual shift inaugurated between analog and digital coding. The Odyssey’s
players complete both its electrical and conceptual circuits, tracing a continuous
line from their embodied experimentation to the logical flow of its program to its
humming hardware. No level is fully self-sufficient, and none can pretend to subsume
the others.
It is no small trick to maintain the enmeshed meta-stability of this multi-level,
multiscalar, multi-modal system. As we have seen, intricate programming that spans
modes, scales, and levels of abstraction is required. Volleyball, as a game, and
the Odyssey, as a platform, are exemplars of what we might call multi-level coding.
This style of programming addresses multiple scales simultaneously, exchanging information
between them, and thereby weaving a tapestry of digital states, analog contours, natural
language instructions and machine instructions, physical affordances and symbolic
transformations. As we have argued, Volleyball’s code is not reducible to any one
of these strands; it only comes into focus as a human-computer assemblage when all
are considered and traced as enmeshed processes.
The Odyssey challenges not only our common assumptions about the strict programmatic
separation between the analog and the digital, but also the role of video games in
computational history. Volleyball makes a compelling case for early video games as
far more innovative and consequential than as merely one subsidiary category of home
software focused on self-contained simulations. Volleyball is porous rather than
self-contained, a program that enters and incorporates the material world rather than
a hermetically sealed digital simulation. Players have to do far more than learn
the algorithms of the system and optimize their performance within it: here they become
active authors in the primary program loop, actualizing and sustaining the code as
if they were part of the hardware platform — which indeed they are. The Odyssey may
not attempt to teach its players anything about formal computer programming, but it
does teach them how to integrate with, realize, and tweak complex human-computer systems
that render commensurate radically disparate scales and modes. Far from being merely
primitive versions of later digital simulations, the generation of games to which
Volleyball belongs were charting a radical path devoted to bringing worlds together
and teaching their players how to sustain these new, hybrid human-computer assemblages.
Conclusion
We have traced an unusual program coded for a mostly forgotten platform as a deliberately
provocative edge case for critical code studies, and academic study in general. Not
everyone, we think, would agree that this program constitutes code at all, if we insist
on defining code as discrete symbolic characters that are encoded in a binary system
and compiled for general processors consisting of transistorized logic gates. However,
we would argue that none of these features are necessary for a program to be considered
code. As we have shown, even extremely limited-purpose analog computer programs possess
the same logic operations, abstract layers, and semantic context as digital code.
The fact that Volleyball does not prioritize any particular level of abstraction nor
set of linguistic conventions (a defined programming language) does not make it any
less of a formally coded system. We have argued that its functions are distributed
across multiple modes, layers of abstraction, and scales that function as dynamic
and mutually constitutive levels, all of which are required for the program to generate
meaning and become operationalized at all. It thus charts a new set of potentials
for human-computer interaction, formalizing them as the user-sustained, coded loops
we now know as video games.
Video games were (and are) at the vanguard of human-computer interaction and mutual
composition. Instead of viewing them as typical code wrapped in layers of input-output,
we can consider them as prime examples multi-level code, variously materializing themselves
across boundaries, bouncing from level to level, environment to environment, expanding
with each bounce the terrain upon which code can operate. While we mean to draw attention
to the underrepresentation of analog programs, so prevalent historically, in scholarly
discourse about code, computers, and media, we also point to the potential of even
software of the more common sort — digitally coded in alphanumeric form in a programming
language oriented within a software stack — to reactivate these active, self-reflexive
relationships through multi-level coding.
If video games proper are only one particularly self-reflexive expression of a more
generalized gamespace that governs our actions at all levels, from database structure
(Horton 2021, 185) to social interfaces (Galloway 2012) to planetary scale computing
(Bratton 2016), then renewed attention is due to the analog-digital hybrid loops formed
by game-like coded systems, including especially the boundary objects that are both
produced and exploited by these systems.
Volleyball and the Magnavox Odyssey remind us that code too can be fuzzy, that it
may require a breakdown of the distinction between inside and outside, even if it
also means giving up the ability to pin code down to a particular scale, level, or
mode. We would be hard pressed to define a bright boundary for Volleyball’s code,
a critical threshold between that which is inside the code and that which is external
to it. It is commonplace to assume that code is neatly contained within its own self-defined
representation, hermetically sealed from environments it doesn’t internally define
or model. Perhaps we receive this conception of code from the conventions of singular
files and their representation within operating systems and digital file systems.
We say that a program is run on hardware (implying a strong logical separation), and
that interfaces mediate between input, code, and output. In the case of Volleyball,
we have shown that though we can analytically differentiate between levels or modes
of expression, we cannot isolate code at any particular one of them and hope to produce
a complete explanation of how it runs. Volleyball works, or alternately “crashes,”
by expressing itself as a distributed, multi-scalar system. This program belongs
to a special class of analog programs that are rare today[17], but we suggest that these insights can be applied to other programs, analog and
digital, as well.
We are arguing for a version of code and coding as mutational, material, and transitive,
that can run on multiple levels simultaneously, and thus composes a platform, along
with hybrid objects and their attendant subjects. In this sense, the program we have
explored here resists Kittler’s distinction between hardware and software, the programmable
and the non-programmable, and thus does indeed manage not only to “keep up with” the
dynamics of the material world, but helps to compose and shape them. Digital code
may not reduce to signifiers of the physical world so much as it expands to incorporate
them. Abstraction doesn’t necessarily hide materiality; it can couple with it to
form multi-leveled systems with joint characteristics of the natural environment and
syntactic procedural organization. This is, in fact, how code got its teeth, and
why it matters as a social and political actor.
If there appears to be something humble about analog programming, it is because it
cannot pretend to totality. If the digital computer, “like any good universal solvent,
has dissolved its own container and vanished from sight” (Haigh 2019, 1) and is thus
capable, in principle and in neoliberal ambition, of swallowing up everything else,
establishing a gamespace that “dynamites everything that is not in the game, like
an outdated Vegas casino” (Wark 2007, 009), then Volleyball, from the dawn of video
games and the twilight of analog computation’s golden age, provides a fascinating
countermodel to hegemonic coding. Instead of either contributing to the quantification
and programmability of the analog world (capture, encoding, simulation) or enacting
hacks that challenge digital capital’s totality or sovereignty (the exploit, gaming),
Volleyball exists on a different axis. Its function, in our reading, is to explore
the possibility of a milieu that isn’t collapsed on one side by an all-encompassing
digital media that enrolls its users as data or on the other by coders and players
who consume the digital as a means of manipulating simulated worlds. Volleyball is
not a simulation of its titular sport, but rather an analog of world making.
References
(Abelson and Sussman 1996) Abelson, H. and Sussman, G. J. Structure and Interpretation
of Computer Programs. The MIT Press, Cambridge, Massachusetts. (1996)
(Baer 2005) Baer, R.H. Videogames: In the Beginning. Rolenta Press, Springfield, NJ.
(2005)
(BNL History) The First Video Game? (WWW Document), n.d. . BNL History. URL https://www.bnl.gov/about/history/firstvideo.php (accessed 6.8.21). n.d.
(Bogos 2009) Bogost, N.M. Racing the Beam: The Atari Video Computer System. The MIT
Press. (2009)
(Bratton 2016) Bratton, B. The MIT Press, Cambridge, Massachusetts. (2016)
(Brown and Vranesic 2009) Brown, S. and Vranesic, Z. Fundamentals of Digital Logic
with VHDL Design, Third edition. McGraw-Hill, New York, New York. (2009)
(Coin 2016) Coin, E. More Analog Computing Is on the Way (WWW Document). dzone.com.
URLhttps://dzone.com/articles/more-analog-computing-is-on-the-way
https://dzone.com/articles/more-analog-computing-is-on-the-way (accessed 6.6.21). (2016)
(Galloway 2006) Galloway, A.R. Gaming: Essays On Algorithmic Culture, First edition.
Univ Of Minnesota Press, Minneapolis. (2006)
(Galloway 2012) Galloway, A.R. Polity, first edition. Cambridge, UK (2012)
(Gilliland 1967) Gilliland, M.C. Handbook of Analog Computation. Systron-Donner Corp.
(1967)
(Haigh 2019) Haigh, T. Introducing the Early Digital, in: Exploring the Early Digital.
Springer, New York, NY. (2019)
(Holst 1982) Holst, P. George A. Philbrick and Polyphemus: The First Electronic Training
Simulator. undefined. (1982)
(Horowitz and Winfield 2015) Horowitz, P. and Winfield, H. The Art of Electronics,
Third edition. Cambridge University Press, New York, New York (2015)
(Horton 2021) Horton, Z. The Cosmic Zoom: Scale, Knowledge, and Mediation. University
of Chicago Press, Chicago, Illinois (2021)
(Hou Je Bek 2008) Hou Je Bek, W. Loop, in: Fuller, M. (Ed.), Software Studies: A Lexicon.
The MIT Press, Cambridge, Mass, pp. 179–183. (2008)
(Huskey and Korn 1962) Huskey, H.D., Korn, G.A. Computer Handbook. Edited by H.D.
Huskey ... and G.A. Korn, Etc. McGraw-Hill Book Company. (1962)
(Khalil 2002) Khalil, H. K. Nonlinear Systems, Third edition. Prentice Hall, Upper
Saddle River, New Jersey, (2002)
(Kittler 1997) Kittler, F.A. There Is No Software, in: Johnston, J.H. (Ed.), Literature,
Media, Information Systems. GB Arts International, Amsterdam, pp. 147–155. (1997)
(Kline 2019) Kline, R.R. Inventing an Analog Past and a Digital Future in Computing,
in: Haigh, T. (Ed.), Exploring the Early Digital, History of Computing. Springer International
Publishing, Cham, pp. 19–39. https://doi.org/10.1007/978-3-030-02152-8_2 (2019)
(Korn 1952) Korn, G.A., Korn, T.M. Electronic Analog Computers. McGraw-Hill. (1952)
(Heiserman 1978) Heiserman, D.L. How to Design & Build Your Own Custom TV Games. Tab
Books, Blue Ridge Summit, Pennsylvania. (1978)
(LaMothe 1995) LaMothe, A. Black Art of 3D Game Programming. Waite Group Press, Corte
Madera, California. (1995)
(Lessig 2006) Lessig, L. Code, Version 2.0. Basic Books. (2006)
(Lundberg 2005) Lundberg, K. The history of analog computing - Introduction to the
special section. Control Systems, IEEE 25, 22–25.https://doi.org/10.1109/MCS.2005.1432595
https://doi.org/10.1109/MCS.2005.1432595 (2005)
(Magnavox 1972) The Magnavox Company, Volleyball instruction sheet. The Magnavox Company,
Fort Wayne, Indiana (1972)
(Magnavox 1974) The Magnavox Company, 1TL200 Odyssey Game Simulator. Magnavox Service
Manual, Fort Wayne, Indiana. (1974)
(Montfort et al. 2012) Montfort, N., Baudoin, P., Bell, J., Bogost, I., Douglass,
J., Marino, M.C., Mateas, M., Reas, C., Sample, M., Vawter, N. 10 PRINT CHR$(205.5+RND(1)); :
GOTO 10. (2012)
(O’Neil 2017) O’Neil, C. Weapons of Math Destruction: How Big Data Increases Inequality
and Threatens Democracy, Reprint edition. ed. Crown, New York. (2017)
(Patterson and Hennessy 2014) Patterson, D. A. and Hennessy, J. L. Computer Organization
and Design, Fifth edition. Morgan Kaufmann, Waltham, Massachusetts. (2014)
(Pressman and Marino 2015) Pressman, J., Marino, M.C., Douglass, J. Reading Project:
A Collaborative Analysis of William Poundstone’s Project for Tachistoscope {Bottomless
Pit}, 1st edition. ed. University Of Iowa Press, Iowa City. (2015)
(Sedra and Smith 2015) Sedra, S. S., Smith, K. C. Microelectronic Circuits, Seventh
edition. Oxford University Press, New York, New York. (2015)
(Tenenbaum and Pollard 1985) Tenenbaum M. and Pollard H., Ordinary Differential Equations.
Dover Publications, New York, New York. (1985)
(Thomas et al. 2012) Thomas, R. E., Rosa, A. J., and Toussaint, G. J., The Analysis
& Design of Linear Circuits, Seventh edition. John Wiley & Sons, Hoboken, New Jersey.
(2012)
(Ulmann 2019) Ulmann, B. Analog Computer Development in Germany With a Focus on Telefunken
(Scanning Our Past). Proceedings of the IEEE 107, 1763–1771.https://doi.org/10.1109/JPROC.2019.2926611
https://doi.org/10.1109/JPROC.2019.2926611 (2019)
(Vee 2017) Vee, A. Coding Literacy: How Computer Programming Is Changing Writing.
The MIT Press. (2017)
(Wark 2007) Wark, M. Gamer Theory. Harvard University Press, Cambridge, Mass. (2007)
Notes
[1]
Should we call some things in L1 affordances? Right now there is no mention till L2
[2] A total of 28 games were released for the Odyssey before its discontinuation
in 1975, including two 4-packs after Volleyball’s.
[3]
How does this new text strengthen the throughline argument? Maybe I’m missing it.
If we just want to say there is an overlay then does it require this much to mention
it and refer to the figure?
[4]
Not confident with this suggestion but architecture usually refers to design patterns
used to create large circuits and is featured in courses titled things like “computer
architecture”.
[5]
I understand the definition that follows but not the term
[6]
This word is not used again until the very end, where it is defined in the context
of the essay. Maybe some explanation here would be helpful?
[7] Similar concerns had led Willy Higenbothem to program the world’s first real-time
video game, Tennis For Two, on an analog computer at Brookhaven National Laboratory
in 1957 (BNL History).
[8] This unusual 3-pole switch means that the press of a single button by the player
can trigger up to three different circuits in the hardware.
[9] Nick Montfort and Ian Bogost’s groundbreaking book in platform studies, Racing
the Beam, takes its title from exactly this operation, necessitated by the lack of
a frame buffer. They detail many ways in which the lack of frame buffer impacted
both the capabilities of the Atari VCS and the lengths that programmers had to go
in order to code for the platform (Bogost and Montfort 2009, 27).
[10]
This and the next 6 lines of edits by me were from a previous revision it seems
[11] KVL states that the sum of voltages in any closed loop of the circuit equals
zero. KCL states that the sum of currents through any node (group of connected device
terminals) is zero (Horowitz and Winfield 2015, 2)
[12]
In the above I’m trying to make the case that a higher level language is needed to
effectively program the Odyssey. In what’s below you are saying that the digital system
is inherently an approximation. So we would need some kind of transition between these
points or remove one.
[13]
That grid will usually be the 7-15 digits of scientific notation I mentioned above,
not usually the grid on the screen, though older digital consoles did discretize position
at the screen resolution
[14]
How does this paragraph fit into the argument matrix? While it is valid, the uses
of anti-aliasing and floating point numbers make the differences basically ontological,
like the audiophile analogy from earlier in the essay
[15] In fact the ball becomes a torpedo in another Odyssey game, Submarine. In that
game, it is programmed to never disappear, but rather to cause the player spot to
disappear when the two make contact.
[16] It is important to emphasize here that though the Odyssey development team
faced cost constraints, which functions were offloaded to players via natural language
code and which were dictated as machine instructions were the result of deliberate
choices, not inherent platform limitations. The Odyssey could certainly have been
programmed to simulate gravity, just as it simulates lateral ball movement.
[17] Nonetheless, analog computing may be poised for something of a comeback in
the future as computers shrink to the nanoscale. For introductory glosses of the
ways that analog computing has been envisioned in the twenty-first century, see (Lundberg
2005) and (Coin 2016).
Works Cited
URL: https://dhq.digitalhumanities.org/editorial/000827/000827.html
Comments: dhqinfo@digitalhumanities.org
Published by: The Alliance of Digital Humanities Organizations and The Association for Computers and the Humanities
Affiliated with: Digital Scholarship in the Humanities
DHQ has been made possible in part by the National Endowment for the Humanities.
© 2025 the author
Unless otherwise noted, the DHQ web site and all DHQ published content are published under a Creative Commons Attribution-NoDerivatives 4.0 International License. Individual articles may carry a more permissive license, as described in the footer for the individual article, and in the article’s metadata.
Comments: dhqinfo@digitalhumanities.org
Published by: The Alliance of Digital Humanities Organizations and The Association for Computers and the Humanities
Affiliated with: Digital Scholarship in the Humanities
DHQ has been made possible in part by the National Endowment for the Humanities.
© 2025 the author
Unless otherwise noted, the DHQ web site and all DHQ published content are published under a Creative Commons Attribution-NoDerivatives 4.0 International License. Individual articles may carry a more permissive license, as described in the footer for the individual article, and in the article’s metadata.
